The NaijaCoder (http://naijacoder.org) team has come up with a syllabus that we hope can touch on different aspects of computer programming and, more importantly, inspire the students to continue learning on their own.

Daily Checkups

The instructors plan to give out daily exercises to the students to make sure that they understood and, sufficiently, digested the material. The emphasis will be on the quality of the syllabus to help the students (given their varied backgrounds) and not the quantity. The main reference textbook, for now, will be “Introduction to Algorithms” by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. At the end of every day/week, the instructors plan to send out a survey so that feedback can be incorporated into future versions of the syllabus.

Motivational Videos

When I was in high school, I would get bored easily if I didn’t understand why I should learn a concept or tool. So the instructors plan to motivate some programming concepts with some videos by creators (e.g., see this video by Marian Croak sharing her pioneering work on Voice over Internet Protocol https://www.youtube.com/watch?v=OignKQOJT-U).

Fun

This might be the most important part of the program! We hope they can have fun and that some of them could end up creating a video game in some programming language. In addition, daily group lunches could provide some nice camaraderie.

Recently, I have been fascinated by a computer science problem that has to do with solving a system of linear equations given memory constraints. One could also consider what constraints you can impose when the physical medium is changed. i.e., instead of representing a computer using bits, what happens when qubits are used instead? What tradeoffs result?

A quantum bit (qubit) is the basic information unit in a quantum computer. Around 2018, a took a class at Harvard about quantum computing and learned a lot. But I have since moved on to other topics and now find myself in need of a quantum computing refresher. Here are two books I purchased that seem to have a good amount of background material on quantum computing and that I have enjoyed thus far: “Classical and Quantum Computation” by A. Yu. Kitaev, A. H. Shen, and M. N. Vyalyi (2002) [1] and “Quantum Computing: A Gentle Introduction” by Eleanor Rieffel and Wolfgang Polak (2011).

The first book “Classical and Quantum Computation” seems to be an extensive and comprehensive textbook that delves into both classical and quantum computing. It offers a rigorous treatment of the mathematical foundations, algorithms, and complexity theory of these computational paradigms. Part 1 of the book is dedicated to classical computation, part 2 to quantum computation, and part 3 to solutions to problems in earlier parts of the book. My personal opinion is that the intended audience of this book are readers with a strong mathematical and computational background.

The second book “Quantum Computing: A Gentle Introduction” takes a more accessible and approachable route to introduce the world of quantum computing. The book might cater to readers with limited knowledge of advanced mathematics and physics, presenting the core principles and applications of quantum computing in a clear and intuitive manner. This book was written for a broader audience and might be a gentle entry into the subject.

Seems like you can’t go wrong with either book but someone recently asked me about the two books and I wanted to write up my initial thoughts while briefly juxtaposing the two books.

References

[1] A. Yu. Kitaev, A. H. Shen, and M. N. Vyalyi. 2002. Classical and Quantum Computation. American Mathematical Society, USA.

[2] Eleanor Rieffel and Wolfgang Polak. 2011. Quantum Computing: A Gentle Introduction (1st. ed.). The MIT Press.

Simply put, the problem of quantile estimation has to do with estimating the empirical or population cumulative distribution function (CDF) of a sample or a distribution. The amount of information or samples the estimator needs is determined by how many times we will need to query the CDF and how accurate we need our answers to be. In this short exposition, we will focus on empirical quantile estimation.

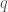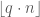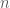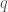We define the -quantile to be the element with rank of amongst elements. The approximate -quantile is any element with rank between 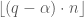and .

Example

Given sample {29, 62, 83, 53, 12, 21, 50, 87, 86, 2}, the 0.1-quantile, 0.2-quantile, and median (0.5-quantile) are 2, 12, 50 respectively. A straightforward way to obtain quantiles is to sort the dataset and the pick the element at the position. This method only works in the offline (non-streaming) setting. For -approximate quantiles, the 0.1-approximate 0.2-quantile consists of the following elements {12, 21, 29}.

Greenwald-Khanna

From previous work [1], it is known that exact computation of quantiles cannot be done in space that is sub-linear in the stream length (if one is allowed at most one pass over the dataset). So one must resort to approximation in order to save space. This becomes especially important when performing analyses on really large datasets — think trillions of data records. In such cases, approximate computation of quantiles in bounded space might be the only feasible solution. Greenwald and Khanna (2001) present a deterministic algorithm for computing approximate quantiles in bounded space. We build on their algorithms to provide private quantiles [2].

With Differential Privacy

Recently, my collaborators and I came up with algorithms for computing DP quantiles in bounded space based upon the Greenwald-Khanna data structure for quantile estimation: (i) Through the exponential mechanism, we sample from intervals defined by the sketch; (ii) We build histograms using the sketch structure. Our algorithms use poly-logarithmic space and are experimentally evaluated on synthetic and real-world datasets [2]. We find that the histogram-based algorithms perform best on more concentrated datasets and for the multiple quantiles problem. In addition, we show theoretical utility bounds specialized to the normal distribution. Our main algorithm uses the exponential mechanism to privately sample from intervals defined by the Greenwald-Khanna sketch.

References

[1] J.I. Munro and M.S. Paterson. Selection and sorting with limited storage. Theoretical Computer Science 12, 3 (1980), 315–323.

[2] Daniel Alabi, Omri Ben-Eliezer, and Anamay Chaturvedi. Bounded space differentially private quantiles. To appear in the Transactions on Machine Learning Research, 2023.

[3] Michael Greenwald and Sanjeev Khanna. Space-Efficient Online Computation of Quantile Summaries. In Proceedings of the 2001 ACM SIGMOD International Conference on Management of Data, Santa Barbara, CA, USA, May 21-24, 2001. 58–66.
https://doi.org/10.1145/375663.375670